Mark Mahowald
| Mark Mahowald | |
|---|---|
| Born | 1931 |
| Nationality | United States |
| Fields | Mathematics |
| Institutions | Northwestern University |
| Alma mater | University of Minnesota |
| Doctoral advisor | Bernard Russel Gelbaum |
| Doctoral students | Michael J. Hopkins |
| Known for | Homotopy groups of spheres |
Mark E. Mahowald (born 1931) is an American mathematician known for work in algebraic topology.
Contents |
Life
He received his Ph.D. from University of Minnesota in 1955 under the direction of Bernard Russel Gelbaum with a thesis on Measure in Groups. In the sixties, he became professor at Syracuse University and around 1963 he went to Northwestern University in Chicago, where he is now a professor emeritus.
Work
Much of Mahowald's most important works concerns the homotopy groups of spheres, especially using the Adams spectral sequence at the prime 2. He is known for constructing one of the first known infinite families of elements in the stable homotopy groups of spheres by showing that the classes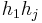 
survive the Adams spectral sequence for 
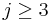. In addition, he made extensive computations of the structure of the Adams spectral sequence and the 2-primary stable homotopy groups of spheres up to dimension 64 together with Barratt, Tangora and Kochman. Using these computations, he could show that a manifold of Kervaire invariant 1 exists in dimension 62.
In addition, he contributed to the chromatic picture of the homotopy groups of spheres: His earlier work contains much on the image of the J-homomorphism and recent work together with Goerss, Henn, Karamanov and Rezk does computations in stable homotopy localized at the Morava K-theory K(2).
Besides the work on the homotopy groups of spheres and related spaces, he did important work on Thom spectra. This work was used heavily in the proof of the nilpotence theorem by Devinatz, Hopkins and Smith.
References
- M. E. Mahowald and M. C. Tangora, Some differentials in the Adams spectral sequence, Topology 6 (1967) 349–369.
- M. G. Barratt, M. E. Mahowald and M. C. Tangora, Some differentials in the Adams spectral sequence II, Topology 9 (1970) 309–316.
- S.O. Kochman and M. E. Mahowald, On the computation of stable stems in The Cech centennial: a Conference on Homotopy Theory, June 22–26, 1993
- M. E. Mahowald, A new infinite family in
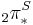, Topology 16 (1977) 249–256. - P. Goerss, H-W. Henn, H.W., M. E. Mahowald and C. Rezk, A resolution of the K (2)-local sphere at the prime 3, Annals of Mathematics 162 (2005), 777–822.